1.即時マグニチュード推定

• 1.1 M9クラスに対応した即時マグニチュード

  
  現在では地震の規模であるマグニチュードは地震モーメントに基づく モーメントマグニチュード が主に使われています．しかし， 津波予報等に用いられる即時マグニチュードは，１分でも早く地震の規模を決 める必要があるため，地震波の振幅に基づく方法もとられています．
  
  地震波振幅に基づくマグニチュードの場合に，用いる地震波の周波数特性のために， マグニチュードの飽和現象が起きます．これは規模が大きな地震ほど断層長が 断層すべりに 長い時間を要するため，放出されてる地震波の周期が長くなることに関係します． 2011年の 東北地方太平洋沖地震では， 断層すべりが始まってから終わるまで約3分かかっています． 地震計により，ドリフトがあまりない 安定して観測するためには，長周期成分を減衰させる必要があります．地震計は， 慣性的に安定した点であるおもりとそのおもりを一定の位置に保つための ばねからできています． 数秒の周期を持つ振り子をつくるのが容易ではないことは想像つくとは思いま すが， 更に長い 継続時間を持つ地震動を正確に計測するのは容易ではありません． このようなことから，地震の 規模が大きく断層すべりの継続時間が長い地震では， 地震計の周期よりも地震動の周期が長くなり，記録された地震波の振幅から 決定される マグニチュードが小さいというマグニチュードの飽和現象が発生します．
  
  そこで，マグニチュード9クラスの破壊継続時間が長い地震にも対応した 即時的なマグニチュード決定法を 開発しました．単純に使う周期帯を長くして100秒周期までの遮断周期にした ものなのですが，このようなマグニチュード決定 法は考案されてきませんでした． 現在では非常に強い地震動は加速度計によって計測されます． 長周期成分について計測しやすい変位振幅として用いようとする場合には， 加速度計の記録を数値 積分して変位記録を得ます．全帯域で一様な分解能を持つ加速度計の 記録を積分して変位振幅とした場合には，長周期になればなるほど ノイズが大ききな特性となってしまい ます．そこである程度より長い周期の成分はディジタルフィルター により減衰させます． 再帰型のディジタルフィルターを用いると処理時間遅れ のないフィルター処理が可能となります． 2011年東北地方太平洋沖地震における地震波形の例を図1に示します． 遮断周期による地震波形の違いがわかります．以前の即時的マグニチュードは遮断周期約5秒 だったのですが，遮断周期100秒の地震波形と比べるとかなり異なった波形となります．
  
  
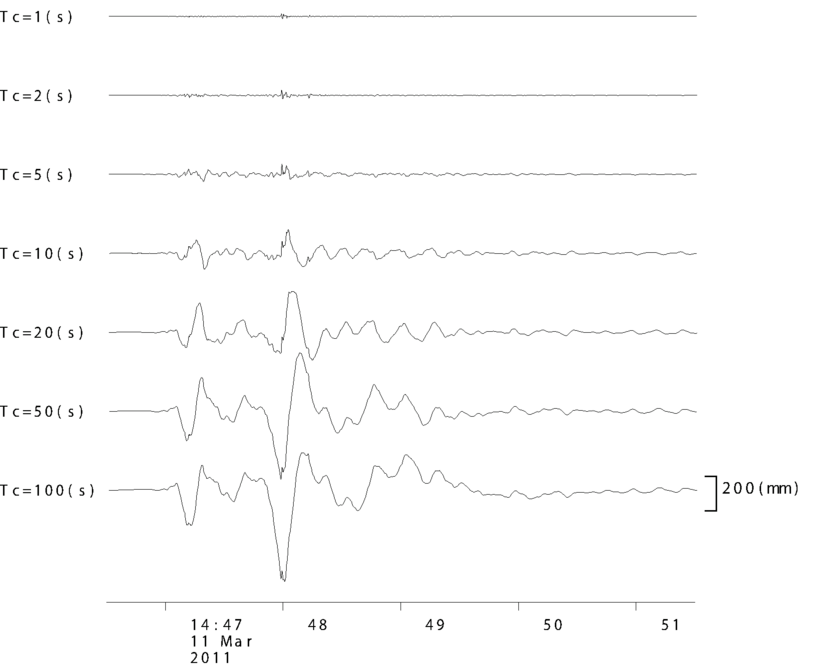
  図1 遮断周期(Tc)の違いによるフィルター処理後の地震波形の違い．
  
  このような地震波形の振幅AをM= a log A +b log D + c のような簡単な式に当てはめて マグニチュード(M)を求めます．ここでDは震源から観測点までの距離です．観 測振幅にあてはめた結果を図2に示します．
  
  
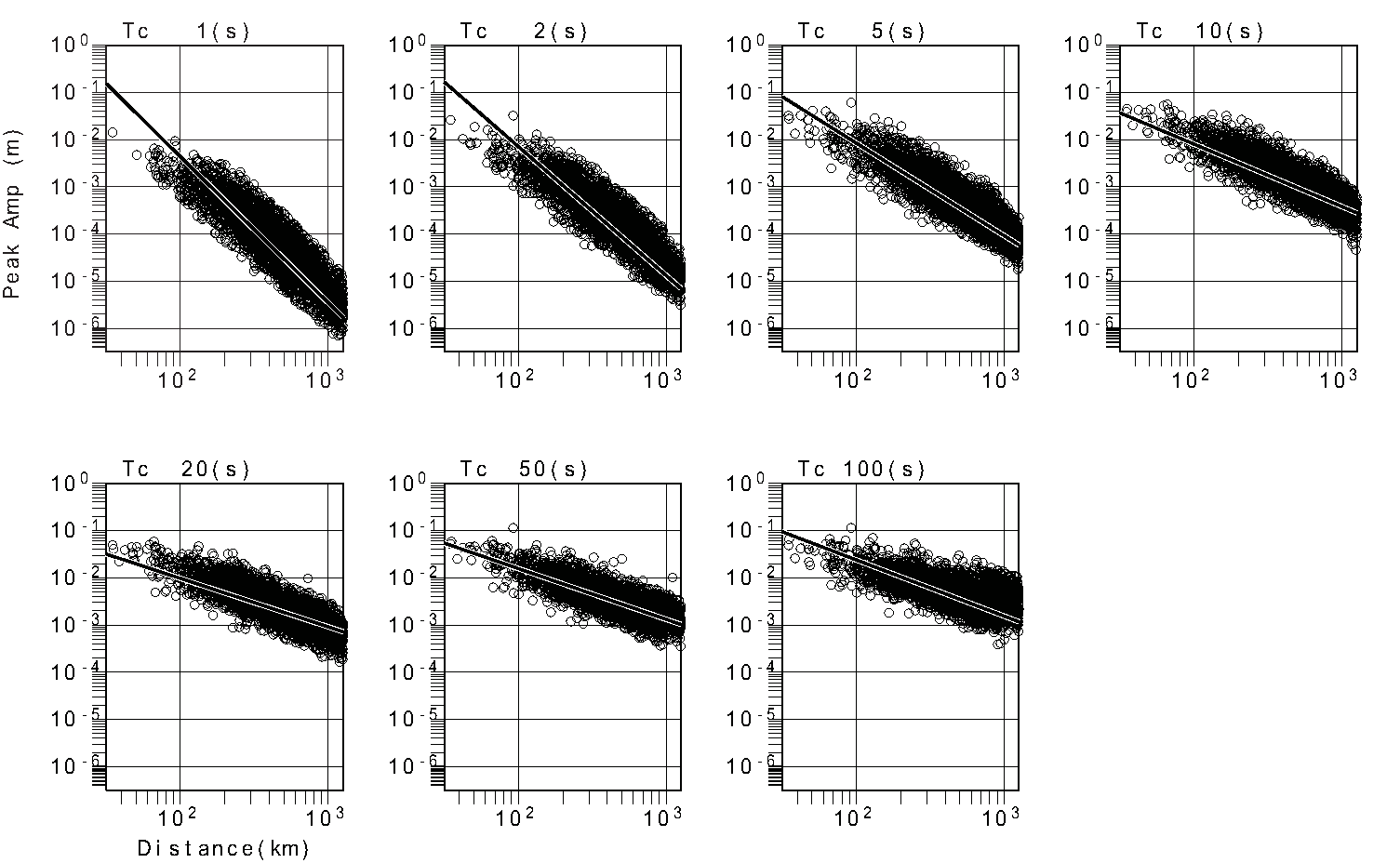
  図2 遮断周期(Tc)の異なる地震波の観測振幅と震源距離との関係．
  
  このような式で計算したマグニチュードの時間変化を図3に示します． 5地震について結果を示しています． 時間が経過するにつれて，推定マグニチュードが次第に大きくなるのは， 時間の経過に伴って断層破壊の範囲が広がっているため，および時間が経過すると 広い範囲の観測点において地震波を計測できるようになることのためにです．
  
  
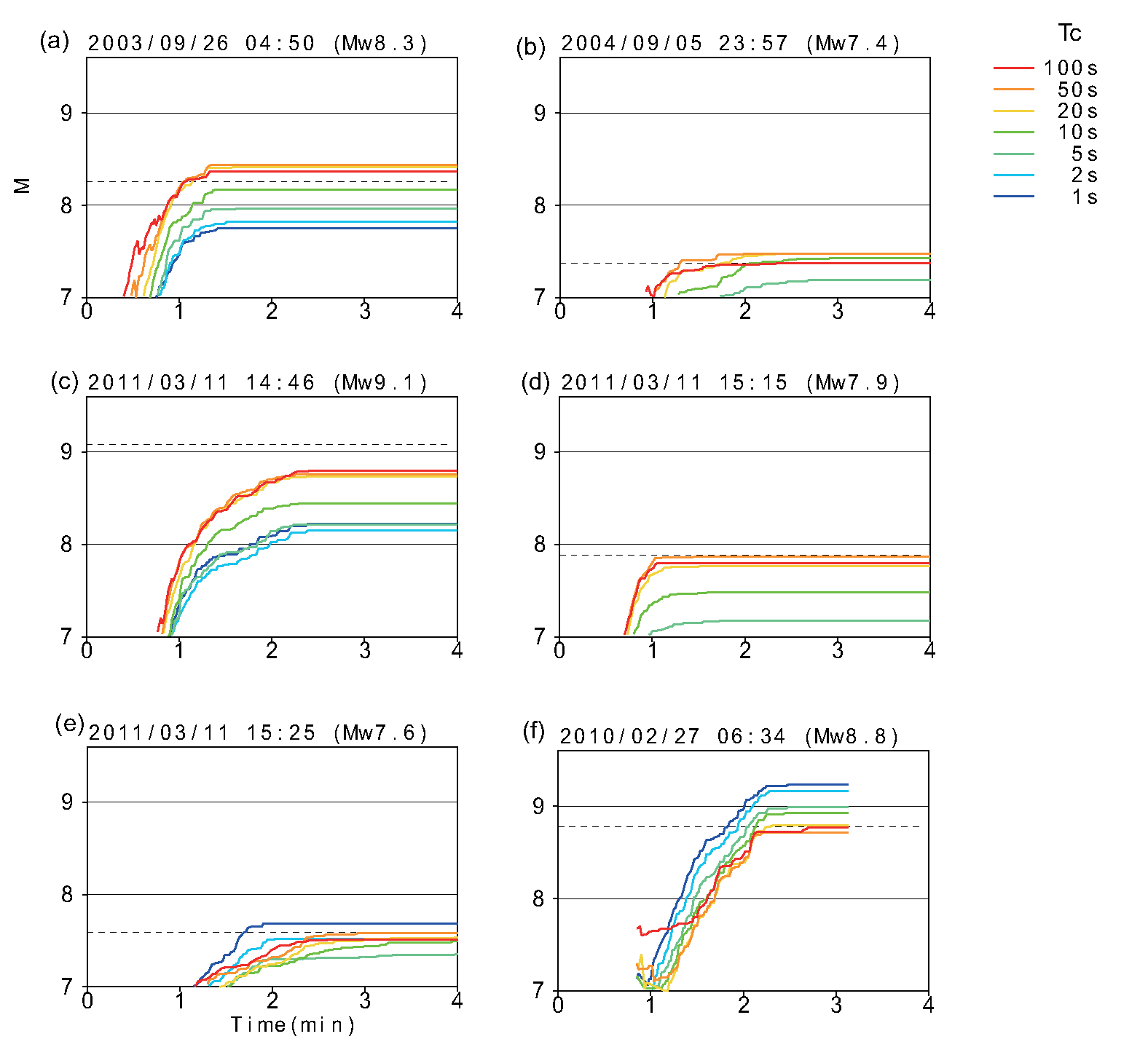
  図3 地震発生後の時間とマグニチュードの値の関係．破線がモーメント マグニチュードの値を示す．(c)が2011年東北地方太平洋沖 地震の例，(f)はチリの2010年マウレ地震の例．
  
  2011年東北地方太平洋沖地震では，断層すべりが始まってから終わるまで約3分かかったと 見られていますが，図3では2分余でマグニチュードが安定化しています． これは，地震波形の変位振幅が 地震モーメントの時間微分（モーメントレート）に比例するとされており， 変位振幅のピークは 断層すべりが終了する前に現れていることに関係しています． また，使用する地震波形は，震央距離が 近い観測点のものに制限していることにも関係しています．
  
  
  

• 1.2 津波地震に対応した即時マグニチュード

  
  津波地震とは，地震動が小さい割に大きな地震を発生させる地震です． 日本では1896年の明治三陸地震の例があります． 世界的には1992年ニカラグア地震，2010年メンタワイ地震などが知られていま す． これらは，海溝付近で発生する応力降下量の小さな地震であるとみられていま す． そのような地震に対して，地震波形振幅に 基づく即時マグニチュードを決めても，マグニチュードが過小に評価 されてしまいます．これは，初期津波 予測の過小評価につながります． そこで津波地震に対応したマグニチュード推定法を開発しました．
  
  単なる振幅だけでなく，震源におけるすべりの継続時間も含めて推定する方法 を 考案しました． ここでは，観測波形と理論波形の周期帯ごとの振幅分布を比較する方法で， 波動源の継続時間を推定する方法をとりました． 図4は横軸に周期，縦軸に振幅を示していますが， 黒が帯域通過フィルターを処理した観測波形の振幅，赤が帯域通過フィルターを処理した理論波形の 振幅を表しています．
  
  
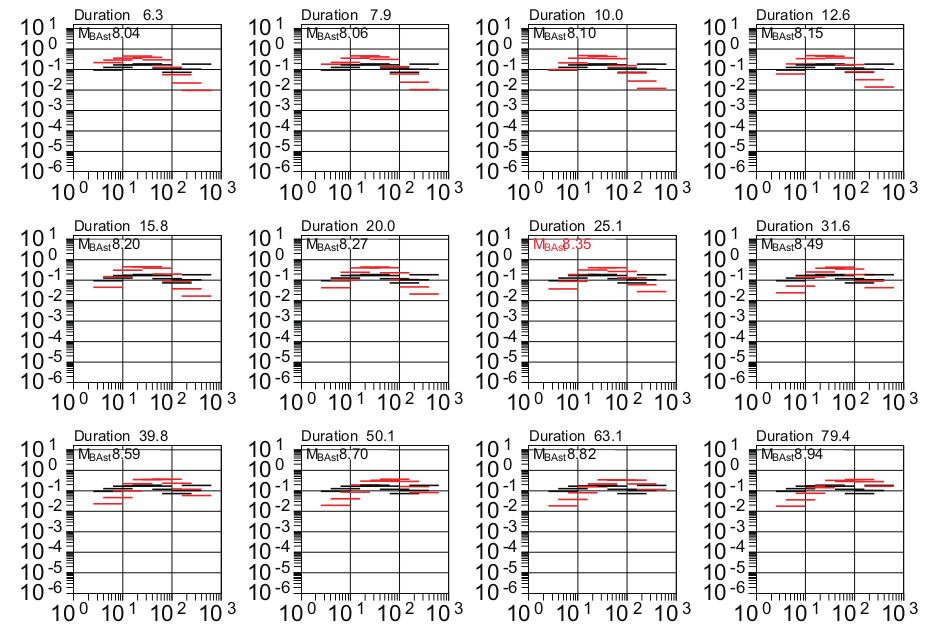
  図4 様々な震源の継続時間(Duration)を仮定した理論振幅分布（赤）と 観測振幅分布（黒）の比較．
  
  この手法を用いて，日本周辺で発生した地震の規模を推定した結果を図5に示します． この手法によるマグニチュードは，モーメントマグニチュードに 比較的近い値が得られていることがわかります． しかし，これらの地震は津波地震ではありません．
  
  
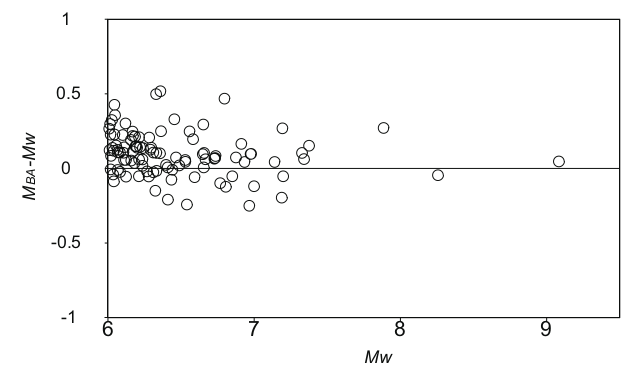
  図5 津波地震用のマグニチュード推定結果とモーメントマグニチュード(Mw)の 関係．
  
  このマグニチュード推定法が，過去の津波地震の規模を適正に推定できるかどうか シミュレーションを行ってみました．実際の観測データについて検証できればよいのですが， この解析には広帯域地震計のデータが必要であり，広帯域地震計のデータが十分得られている 津波地震はあまりありません． 図5に示すように，過去の代表的な5地震について 日本海溝の近くで発生したとして，シミュレーションを行ってみました．その結果，5地震の うち3地震ではモーメントマグニチュードに比べて0.2以内の差，１地震について0.3の差，1地震 については，0.4の差の値が得られた．0.3の差がついた地震は2010年メンタワイ地震ですが，この 地震については，十分な広帯域地震計の観測記録が得られています． この手法を適用したところ， モーメントマグニチュード7.8に対して，マグニチュード7.7が得られました． シミュレーションの結果よりも，実際の結果は差は小さくなっていました． しかし，2006年ジャワ 地震のシミュレーションでは0.4の過小評価となっており，まだ調査が必要で す．
  
  
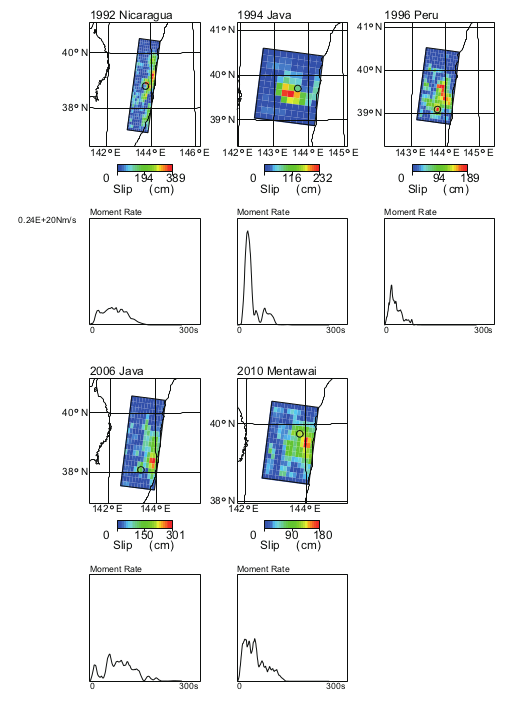
  図6 過去のの津波地震が日本海溝付近で発生したと仮定したシミュレーション． カラーマップは各地震のすべり量を示します． これらのすべり量はUSGSが推定した値を参照しています． 各地震の地震モーメントの時間微分量(moment rate)を各地図の下に示しています．