光学

2025年前期 金曜2限＠多目的ホール

テキスト：櫛田孝司 光物理学 共立出版
参考書: 光学の原理　ボルン　ウォルフ著　東海大学出版会
(Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, M. Born, E. Wolf, Cambridge University Press)
光学　ヘクト著　丸善出版
(Optics, Hecht, Pearson Education Limited)

アナウンス

授業での配布プリント、課題、解答、試験情報をこのページに掲示します。
課題に提出上の注意 グラフを描くときの注意
  1. グラフ用紙, 定規を用いて丁寧に描く.
  2. 軸の名前や単位を明確に示す. 軸に必要な数値を明確に示す.
  3. 離散的なデータでは，点(印)のみで描く. 不必要に点と点を線で結ばない.
  4. 2つ以上の異なる系列のデータを一つのグラフに描くときは, 点の記号や線の種類を変える. また, 凡例を付ける.

期末試験の予定

期日: 8/1 (金) 2限
会場: 多目的ホール
筆記用具のみ持ち込んで下さい. 定規を持参して下さい.

授業内容

シラバス
  1. 光物理学の概要
    課題1 提出日 4/18(金) 2限初め

  2. 幾何光学
    課題2 提出日 4/25(金) 2限初め 問題をA4用紙に印刷して回答してください. 略解付の問題は提出前に自ら採点，修正して下さい. 略解2

    課題3 反射 提出日 5/2(金) 2限初め略解

    課題4 屈折 各自取り組みましょう。略解 略解付の問題は提出前に自ら採点，修正して下さい. 提出日 5/9(金) 2限初め

    課題5 レンズ 略解 略解付の問題は提出前に自ら採点，修正して下さい. 提出日 5/16(金) 2限初め

    厚レンズの公式導出例

    課題6 共軸球面光学系 略解 略解付の問題は提出前に自ら採点，修正して下さい. 提出日 5/23(金) 2限初め

    5/30(金) 小テスト これまでの内容や作図について復習しておいて下さい.

    課題7 略解 略解付の問題は提出前に自ら採点，修正して下さい. (問1.(3)は省略してかまいません) 提出日 5/30(金) 2限初め



  3. 波動としての光と干渉

    課題8 各自取り組みましょう. 6/13 小テストを行います 略解.

    • 波の重ねあわせ
      (1) 波数の大きさ，角振動数が等しい2つの波の重ね合わせ.
      interference
      交差する2つの平面波の合成(本の２波の進行方向のちょうど中間の方向へ進行する波が見える)
      interference
      交差する2つの平面波の合成(定在波の節面が見える)


      (2) 波数の大きさ，角振動数が僅かに異なる2つの波の重ね合わせ

      2つのアニメで波長の長短の波がどちらへ進んでいるかに注意してみて下さい.
      左図: 長短の2波は同じ速度で同じ方向へ進む.
      右図: 長い波長の波は「　」方向へ, 短い波長の波は「　」方向へ進む. (答え. 左, 右)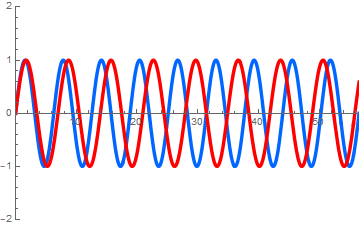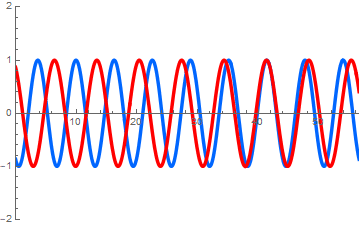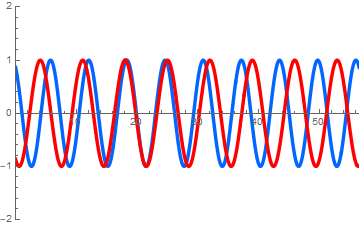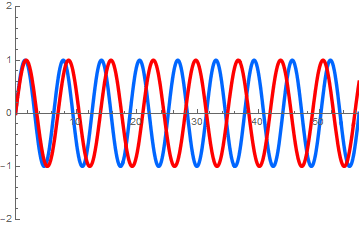
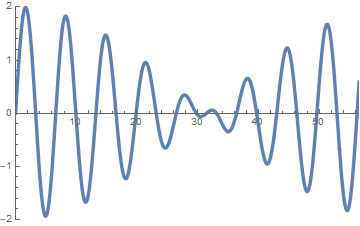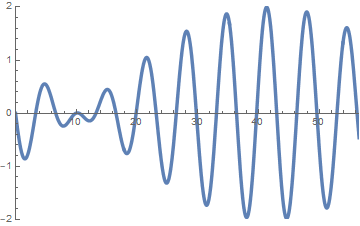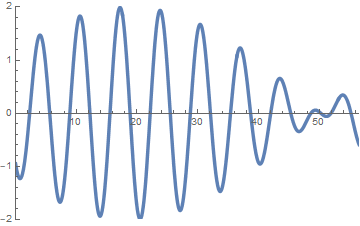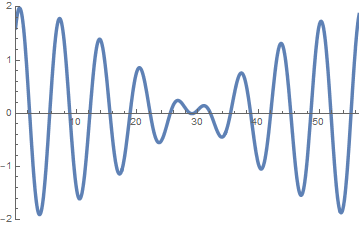
      重ね合わせ1
      重ね合わせ1
      sin(x-t)+sin(0.9x-0.8t)
      重ね合わせ2
      sin(x-t)+sin(1.1 x - 0.9 t)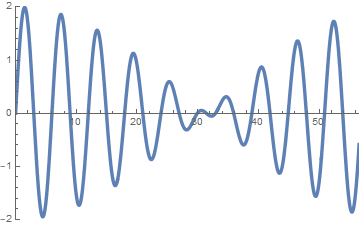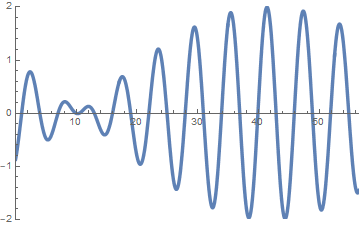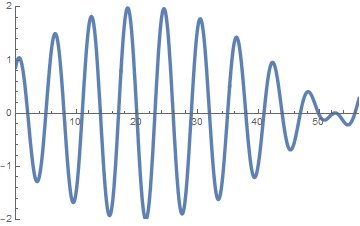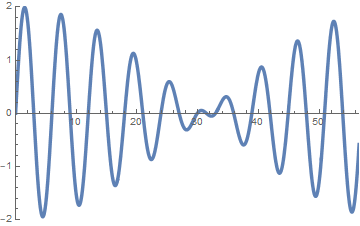
      重ね合わせ2
      sin(x-t)+sin(1.1 x - 0.9 t)


      課題9 波動 各自取り組みましょう. 略解.

    • 干渉
      課題10 干渉 各自取り組みましょう.略解. 6/27 小テストがあります.

      反射による位相変化に興味がある方向け: 例えば,
      砂川重信 理論電磁気学 8章 §4
      Jackson著 Electrodynamics 7.3
      等(図書館にあり)を参照して下さい.

    • 薄膜による干渉
    • 干渉計の利用
    • 天体干渉計
      課題11 各自取り組みましょう.略解

  4. 光の直進性と回折
    • Huygens-Fresnelの原理
      課題12 各自取り組みましょう. 略解
      Fresnel Zone Plateによる集光
      interference interference interference interference interference
      授業中に演示したFresnel Zone Plate(FZP)によるレーザー光の干渉像: 左はFZPの直後, 右に行くにしたがいFZPから遠ざかり，設計焦点での像が右端の写真. 左の写真では中心は暗いが, 右の写真では集光されて明るくなっていることに注意.

    • Kirchhoffの公式
      課題13 各自取り組みましょう。略解

    • Fresnel回折


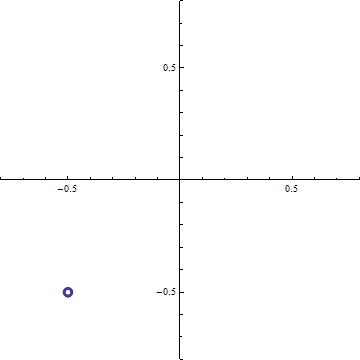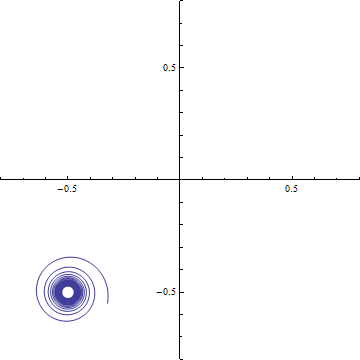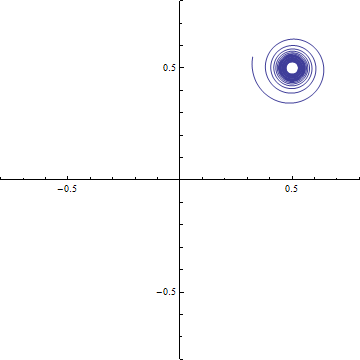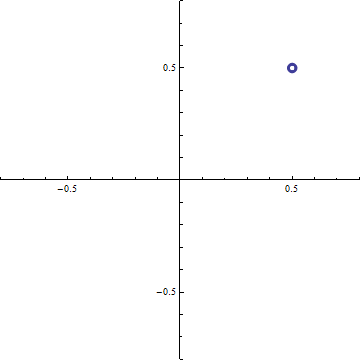
      Cornuの螺旋
       Cornuの螺旋 横軸 C(ξ), 縦軸S(ξ)として ξ=-20〜+20の範囲で描いたもの. (0.5, 0.5), (-0.5, -0.5)の２点に螺旋が巻き付く.


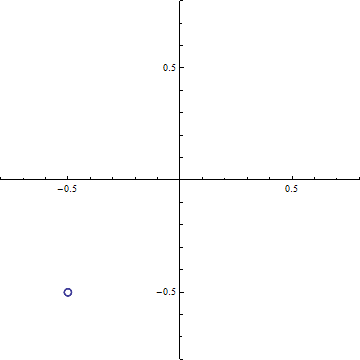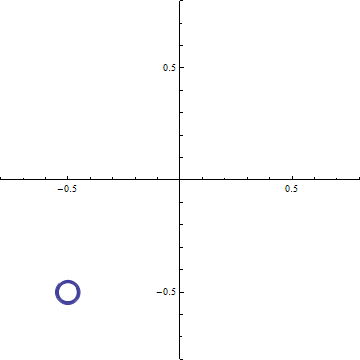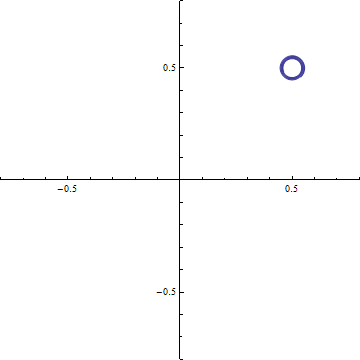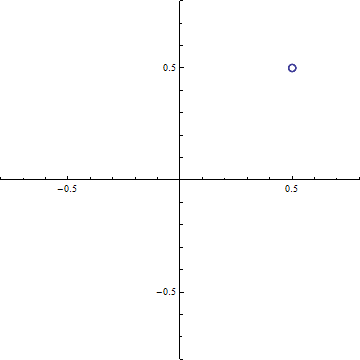
      cornu5
      (a-1) d=5
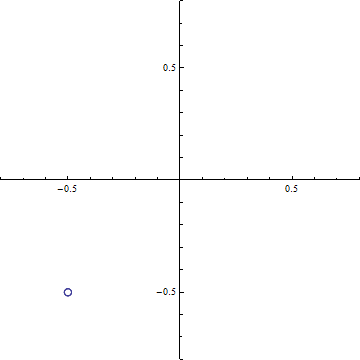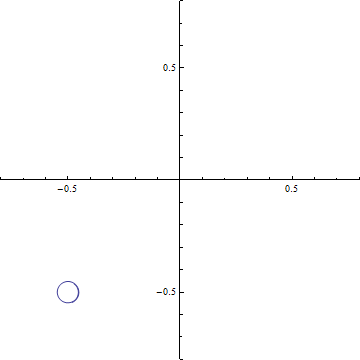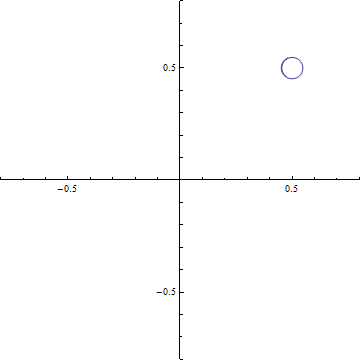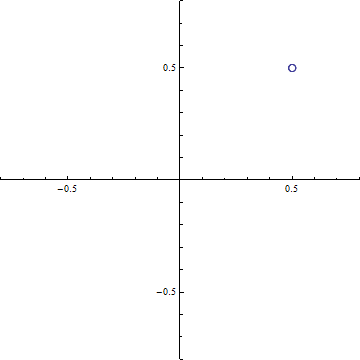
      cornu5
      (a-2) d=1
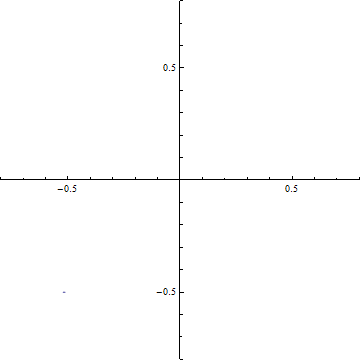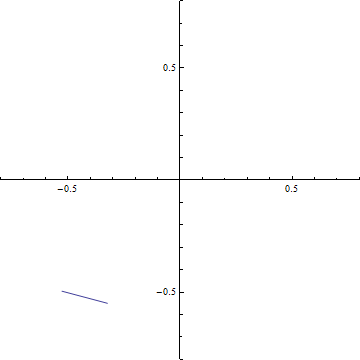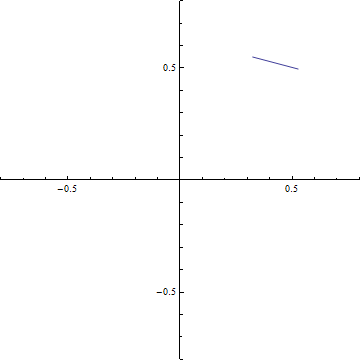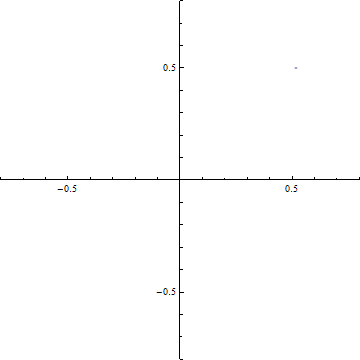
      cornu5
      (a-3) d=0.2
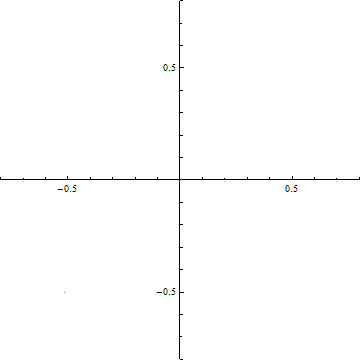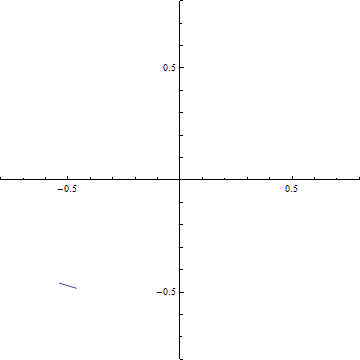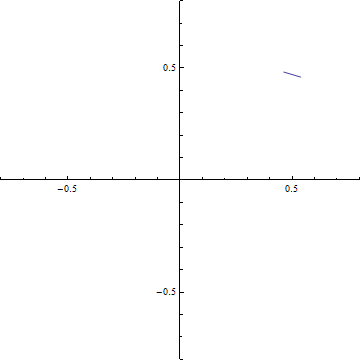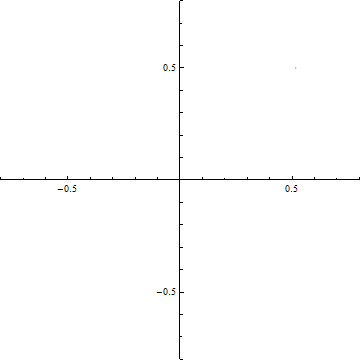
      cornu5
      (b-1) d=5
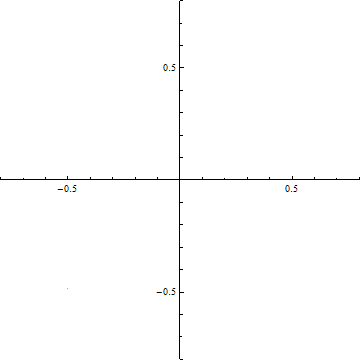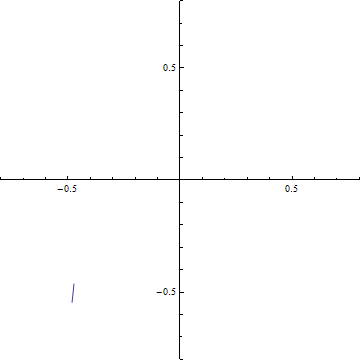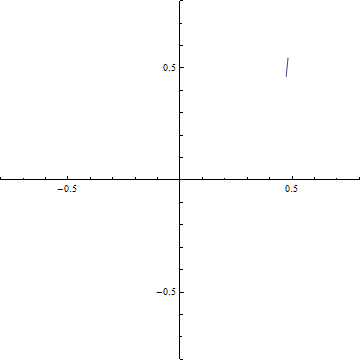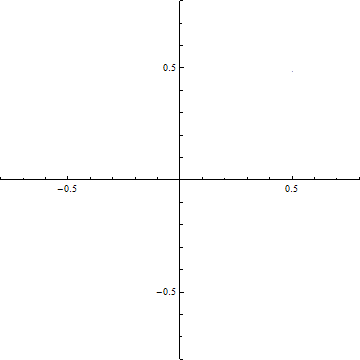
      cornu5
      (b-2) d=1
      cornu5
      (b-3) d=0.2
      cornu5
      (c-1) 回折強度分布 d=5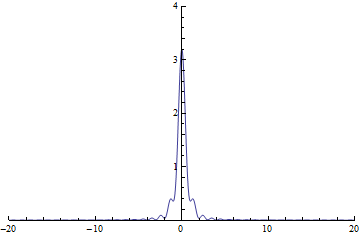
      cornu5
      (c-2) 回折強度分布 d=1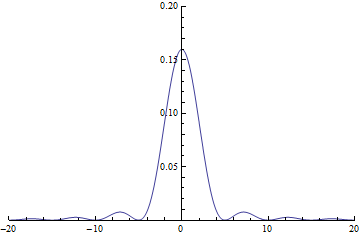
      cornu5
      (c-3) 回折強度分布 d=0.2
      (a)ξ-=t-dからξ+=t+dまでの範囲のCornuの螺旋 (ただし, d=√(R/2R)). 横軸はC(ξ), 縦軸はS(ξ)である. この曲線の両端を結ぶ線分の長さの2乗がΔC2+ΔS2に等しい.
      (b) ξ-=t-dからξ+=t+dまでの範囲のCornuの螺旋の曲線の両端を結ぶ線分．横軸はC(ξ), 縦軸はS(ξ)である.
      (c) 回折強度分布. 横軸はξであり, (b)の長さの2乗からΔC2+ΔS2を求め縦軸としてプロットしたもの.


    • Fraunhofer回折

      課題14 各自取り組みましょう。略解



      スリットによる回折
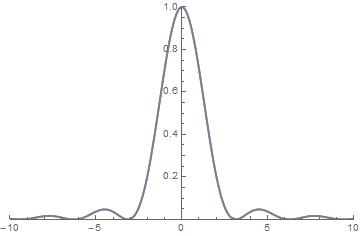
      (1) 単独のスリット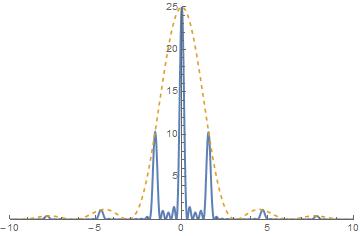
      (2) スリット5個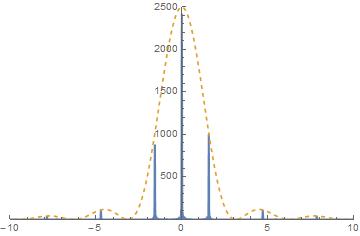
      (3) スリット50個
      複数の同じ幅のスリットによる回折(スリット同士の間隔はスリット幅と等しい)。スリットの個数が増えると，回折光の分布の幅が狭くなる。(2),(3)図の点線は，単独のスリットによる回折光の分布であり，狭い回折分布の包絡線となっている。

      円孔による回折

      課題15 各自取り組みましょう 略解

      円形開口での回折で利用する道具: Bessel関数
      Bessel関数 Jn (青, 赤 緑線の順にn=0, 1, 2)


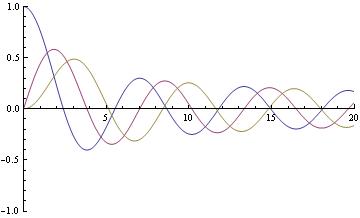
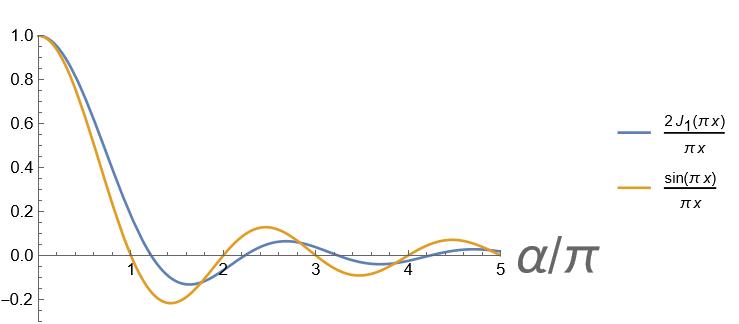
      2 J1(z)/z と sin z /z (青、赤線の順)
      円形開口と矩形開口ではゼロ点(強度がゼロとなる位置)が僅かにずれる. sin z/zのゼロ点は mπ(m=±1,±2,...).
      Bessel関数 J1の最初の零点は1.22 π.