This program is ideal for those who wish to pioneer new fields through the power of mathematics.
In the sciences, many groundbreaking discoveries have been made using new methods that integrate mathematics and informatics. Research aimed at solving social issues is also active, and expectations for the roles of mathematics and information science continue to grow.
Let us open new frontiers together through the combined power of mathematics and informatics.

Curriculum

With the rapid development of computational devices and algorithms, problems once thought to be impossible to compute are now becoming solvable.
For example, many studies have shown that computers can now recognize image data obtained from observations and perform cognitive and decision-making tasks similar to those of humans.
Such advances in data-driven research are transforming the very nature of science itself.

This program offers courses designed to help students understand these cutting-edge developments.
In the second year, students build a solid foundation by studying the fundamentals of mathematics and information science.
In the third year, through courses in Data Science (DS) within the Faculty of Science and interdisciplinary DS courses that connect the sciences and humanities, students learn how the knowledge gained in the previous year can be applied to various fields such as social sciences, natural sciences, and engineering.
They also gain practical skills through problem-based learning.
In the fourth year, students apply what they have learned to conduct their graduation research.

Research Topics

Algorithms for Cell Boundary Extraction by Computer

Here is an example of research that combines mathematics and computer science.
Many living organisms, including humans, are composed of cells as their fundamental units.
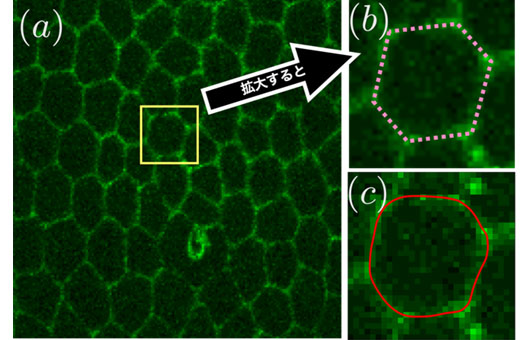
Figure (a) shows a cross-sectional image of a tissue, where you can see structures that resemble soap bubbles.
Each “bubble” actually corresponds to a cell boundary (indicated by the dotted lines in Figure (b)).

Can we train a computer to automatically recognize and extract these cell boundaries? The answer is yes. Figure (c) shows the result of a computational algorithm that successfully extracts the cell boundaries, shown in red.
Traditionally, such tasks required a tremendous amount of manual work, but automated algorithms like this one dramatically reduce processing time.
This research has broad potential applications — for example, understanding the principles of biological morphogenesis or detecting abnormalities in cell shapes that may indicate disease.

Biological Rhythms and the Belousov–Zhabotinsky (BZ) Reaction

Living organisms exhibit a wide range of rhythmic phenomena — such as heartbeats, respiration cycles, and sleep–wake rhythms.
These rhythms are characteristic of life itself, but how do they arise?
Some researchers have proposed that familiar chemical reactions, like those you might have experimented with in high school, may hold the key.

In Figure (a), several chemicals are dissolved in the liquid inside a petri dish.
One of these, ferroin, appears red in its reduced state and blue in its oxidized state, producing a striking concentric pattern.
This chemical process is known as the Belousov–Zhabotinsky (BZ) reaction, and it serves as an experimental model for studying biological rhythmic phenomena.

Although the BZ reaction is highly complex, we can construct a mathematical model by focusing only on the essential variables (see the lower part of the figure).
The computer simulation shown in Figure (b) successfully reproduces key features of the actual BZ reaction.
As this example illustrates, by simplifying complex natural phenomena into manageable mathematical models, we can often uncover their underlying principles.
In this program, students will learn both mathematical modeling and computational simulation techniques to explore such fascinating systems.