Highly abstract modern mathematics continues to evolve toward even greater abstraction, while also seeking new themes rooted in our everyday lives. The Program of Mathematics addresses this trend through two major fields: Mathematical Analysis and Mathematical Informatics.
In Mathematical Analysis, we provide detailed education and research from the perspective of pure mathematics. In Mathematical Informatics, we respond to the needs of the modern age by conducting education and research in information science from a mathematical viewpoint. Would you like to study mathematics with us in the Program of Mathematics?

Curriculum

From the second year onward, students mainly study the three core pillars of pure mathematics — Algebra (numbers and expressions), Geometry (figures), and Analysis (differentiation and integration).
After mastering these fundamental areas, students in their third and fourth years advance to specialized seminars and graduation research, where they engage in higher-level mathematical study and independent research. In these courses, students set their own research themes and deepen their understanding not only of mathematics but also of the broader scientific context. Through presentations and discussions, they experience how their own ideas become logically refined and well-organized.

By completing this curriculum, students will acquire the expertise needed for careers that make use of mathematical knowledge — in education, finance, government, or IT fields.
You might wonder, “Is mathematics really needed in companies?” In fact, many industries today are seeking individuals with broad and flexible knowledge. Mathematics is a discipline that bridges the concrete and the abstract, and the ability to approach and solve problems logically is a skill highly valued in any workplace.

Research Topics

Here are some examples of topics that you may encounter as you progress through the program.

You probably learned the quadratic formula in school. Interestingly, algebraic formulas also exist for cubic and quartic equations. However, for general fifth-degree (and higher) equations, no algebraic formula exists to solve them — a surprising and profound result!
What does it mean to “have no algebraic formula”? The answer becomes clear when you study Galois theory, a branch of algebra.
The icosahedron shown on the right, for example, exhibits a geometric symmetry that can also be explained using algebra. Isn’t it fascinating that algebraic concepts concerning numbers and expressions can lead to the classification of geometric figures?

Now, look at the two formulas below.
The upper one is
1 = 1/1 + 1/3 − 1/2 + …
and the lower one is
2 = 1/1 + 1/3 + 1/5 + …
Both contain the same numbers on the right-hand side — only the order is different. Yet, surprisingly, they converge to different values!
Even more strangely, by rearranging the terms on the right-hand side, the series can be made to converge to any desired value.
This is quite different from the intuitive idea of convergence you may have learned in high school. In university mathematics, you will explore the deep reasons behind this phenomenon.

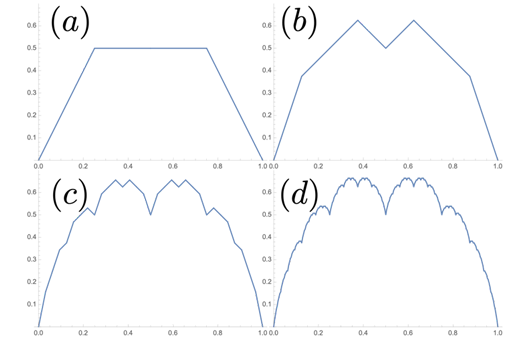
Figure (d) shows the graph of the Takagi function. This function is defined by repeating a certain operation infinitely many times, as shown in figures (a) through (d).
It has some remarkable properties: it is continuous everywhere, yet differentiable nowhere. Its total length is infinite, yet the area it encloses (the blue region bounded by the curve and the lines x=0, x=1, y=0) is finite.
These properties may challenge your intuition about what a “function” looks like. Studying such phenomena requires the rigorous analysis you will learn at university.